<= Get me outta here!

Fermats Little Theorem

By jet/Prussia | 12/08/2023 | code, typescript_javascript, math

I read an article from Quanta Magazine that had this very interesting piece of information:

The basic idea goes back to a result from the 17th-century French mathematician Pierre de Fermat, known as his "little theorem." Fermat considered two integers — call them N and x. He proved that if N is a prime number, then x^N - x is always a multiple of N, regardless of the value of x. Equivalently, if x^N - x is not a multiple of N, then N can't be a prime number. But the inverse statement isn't always true: If x^N - x is a multiple of N, then N is usually but not always prime.

To turn Fermat's little theorem into a primality test, just take the N that you're interested in, choose x at random, and plug the two numbers into x^N - x. If the result is not a multiple of N, then you're done: You know that N is definitely composite. If the result is a multiple of N, then N is probably prime. Now pick another random x and try again. In most cases, after a few dozen tries, you can conclude with near certainty that N is a prime number. "You do this a small number of times," Blais said, "and somehow now your probability of having an error is less than the probability of an asteroid hitting the Earth between now and when you look at the answer."

It reminded me a little of zero knowledge proofs.

Anyways, using Fermat's Little Theorem, I wanted to create a little function that could see whether a number was a prime number or not. First, we had to have a number to check as one of the inputs. And since I was using Javascript, it probably should be a BigInt, so big inputs don't lose any precision. We probably also want to optionally let the caller specify how many checks to do.

Then, for each check, we can generate a random x, calculate x^N - x. If we call that, say, m, then we can do m % N, where % means modulo. If m % N is zero, that means m is a multiple of N, so we continue. If not, then we know the input is not a prime number, and can end it there. If we generate x many times, and m % N is always 0, we can conclude with high probability that the input is a prime.

At first, I mistakenly did N % m === 0, but that means m is a factor (not a multiple) of N, and N would be by definition, not a prime number (assuming m is not or N, as the only factors of a prime number are itself and 1). I realised the problem pretty quickly.

After fixing that, this is the code I had:

function is_prime(potential_prime, iterations=50) {
  for (let i=0; i < iterations; i++) {
    let x = BigInt(Math.floor(Math.random()*10000)); //0 <= x <= 9999
    let m = x**potential_prime - x;
    if (m%potential_prime !== BigInt(0)) {
      return false;
    }
  }
  return true;
}

I tested a random few of the first 1000 prime numbers, and some numbers that were not prime numbers, and it works! Yay!

Just to see if it worked, I tried putting in the very large prime number "531137992816767098689588206552468627329593117727031923199444138200403559860852242739162502265229285668889329486246501015346579337652707239409519978766587351943831270835393219031728127" as a test. And:

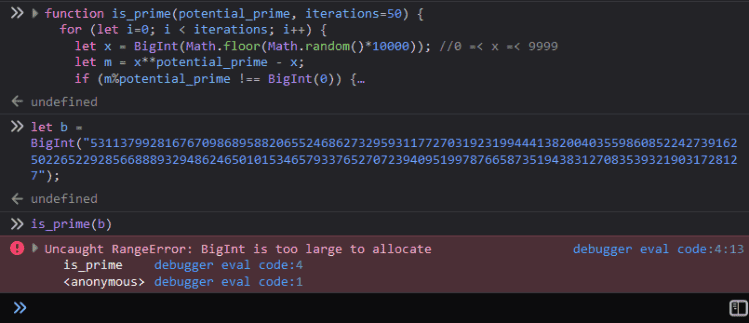
Uncaught range error: BigInt is too large to allocate

...fair enough.

I read an article from [Quanta Magazine](https://www.quantamagazine.org/how-randomness-improves-algorithms-20230403/) that had this very interesting piece of information:


        
          
> The basic idea goes back to a result from the 17th-century French mathematician Pierre de Fermat, known as his "little theorem." Fermat considered two integers — call them `N` and `x`. He proved that if `N` is a prime number, then `x\^N - x` is always a multiple of `N`, regardless of the value of `x`. Equivalently, if `x\^N - x` is not a multiple of `N`, then `N` can't be a prime number. But the inverse statement isn't always true: If `x\^N - x` is a multiple of `N`, then `N` is usually but not always prime.

        
          
> To turn Fermat's little theorem into a primality test, just take the `N` that you're interested in, choose `x` at random, and plug the two numbers into `x\^N - x`. If the result is not a multiple of `N`, then you're done: You know that `N` is definitely composite. If the result is a multiple of N, then `N` is probably prime. Now pick another random `x` and try again. In most cases, after a few dozen tries, you can conclude with near certainty that `N` is a prime number. "You do this a small number of times," Blais said, "and somehow now your probability of having an error is less than the probability of an asteroid hitting the Earth between now and when you look at the answer."

        
          

        
          
It reminded me a little of zero knowledge proofs.

        
          

        
          
Anyways, using Fermat's Little Theorem, I wanted to create a little function that could see whether a number was a prime number or not. First, we had to have a number to check as one of the inputs. And since I was using Javascript, it probably should be a `BigInt`, so big inputs don't lose any precision. We probably also want to optionally let the caller specify how many checks to do.

        
          

        
          
Then, for each check, we can generate a random `x`, calculate `x\^N - x`. If we call that, say, `m`, then we can do `m % N`, where `%` means modulo. If `m % N` is zero, that means `m` is a multiple of `N`, so we continue. If not, then we know the input is **not** a prime number, and can end it there. If we generate `x` many times, and `m % N` is always `0`, we can conclude with high probability that the input is a prime.

        
          

        
          
At first, I mistakenly did `N % m === 0`, but that means `m` is a factor (not a *multiple*) of `N`, and `N` would be by definition, not a prime number (assuming `m` is not or `N`, as the only factors of a prime number are itself and 1). I realised the problem pretty quickly.

        
          

        
          
After fixing that, this is the code I had:

        
          

        
          
```js

        
          
function is_prime(potential_prime, iterations=50) {

        
          
  for (let i=0; i < iterations; i++) {

        
          
    let x = BigInt(Math.floor(Math.random()*10000)); //0 <= x <= 9999

        
          
    let m = x**potential_prime - x;

        
          
    if (m%potential_prime !== BigInt(0)) {

        
          
      return false;

        
          
    }

        
          
  }

        
          
  return true;

        
          
}

        
          
```

        
          

        
          
I tested a random few of the [first 1000 prime numbers](https://en.wikipedia.org/wiki/List_of_prime_numbers#The_first_1000_prime_numbers), and some numbers that were not prime numbers, and it works! Yay!

        
          

        
          
Just to see if it worked, I tried putting in the very large prime number "531137992816767098689588206552468627329593117727031923199444138200403559860852242739162502265229285668889329486246501015346579337652707239409519978766587351943831270835393219031728127" as a test. And:

        
          

        
          
![Uncaught range error: BigInt is too large to allocate](/images/prime_test.png)

        
          

        
          
...fair enough.